Tekanan dan suhu

Artikel ini memberikan jawaban atas pertanyaan-pertanyaan berikut, antara lain:

Apa teori kinetik gas?
Apa asumsi yang menjadi dasar teori kinetik gas?
Bagaimana tekanan gas dijelaskan pada tingkat mikroskopis?
Bagaimana tekanan gas dihitung?
Apa hubungan antara energi rata-rata molekul dan suhu?
Bagaimana energi internal gas ideal ditentukan?

Pendahuluan

Untuk menghubungkan variabel keadaan gas yang diamati secara makroskopis seperti suhu, volume dan tekanan dengan variabel mikroskopis seperti massa partikel dan kecepatan partikel, teori kinetik gas dikembangkan. Dengan bantuannya adalah mungkin, misalnya, untuk menyimpulkan suhu atau tekanan gas dari energi kinetik rata-rata molekul.

Untuk gas (ideal), teori kinetik gas memberikan hubungan penting antara variabel keadaan terukur secara makroskopik (misalnya suhu, tekanan, volume, massa gas, dll.) Dan variabel mikroskopis (misalnya kecepatan partikel, energi kinetik rata-rata, jumlah partikel, parsial massa, dll.)!

Asumsi

Untuk mengembangkan model perilaku partikel gas, beberapa asumsi pertama-tama harus dibuat tentang sifat-sifat gas atau molekul yang dikandungnya. Pertama, diasumsikan bahwa gas adalah gas ideal . Ini berarti khususnya:

partikel gas dianggap sebagai titik massa,
partikel gas tidak mengerahkan kekuatan pengikat satu sama lain,
tumbukan antara partikel gas benar-benar elastis serta tumbukan antara molekul dan permukaan (yaitu tidak ada kehilangan energi)
semua partikel gas bergerak sepenuhnya secara acak, yaitu mereka tidak memiliki arah yang disukai dan karena itu didistribusikan secara statistik di ruang angkasa (yaitu pengaruh gravitasi pada molekul diabaikan).

Interpretasi mikroskopis dari tekanan gas

Pembentukan tekanan gas

Dalam artikel "Tekanan gas", pembentukan tekanan gas telah dijelaskan secara rinci menggunakan model partikel. Tekanan gas yang dapat diukur secara makroskopis ("gaya per unit luas permukaan") dapat dijelaskan pada tingkat mikroskopis dengan cara tumbukan. Jika partikel gas bertabrakan dengan permukaan (misalnya dinding wadah), mereka mengerahkan kekuatan yang mirip dengan bola tenis yang dilemparkan ke raket.

Tekanan dalam gas disebabkan pada tingkat mikroskopis oleh tumbukan partikel yang terkandung di dalamnya, yang bertabrakan dengan permukaan yang berdekatan dan dengan demikian mengerahkan kekuatan tumbukan!

Jika, misalnya, gas di bawah tekanan tinggi tertutup dalam sebuah silinder, partikel yang terkandung di dalamnya bertabrakan terus-menerus dengan dinding silinder dan mengerahkan kekuatan. Gaya tumbukan ini dapat dirasakan dengan jelas ketika, silinder ditutup dengan piston.

Animasi di bawah ini secara skematis menunjukkan tabrakan antara molekul gas dan permukaan piston. Berbeda dengan animasi, karena jumlah besar partikel yang biasanya terkandung dalam gas, orang tidak akan merasakan "memalu" partikel tetapi akan merasakan kekuatan konstan.

Gaya (F) diperlukan untuk menjaga piston pada posisi semata-mata karena tumbukan antara partikel gas dan permukaan piston (A), yaitu tekanan gas! Dari definisi tekanan sebagai "gaya per satuan luas permukaan", tekanan gas (p) akhirnya dapat ditentukan sebagai berikut:

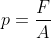$p=\frac{F}{A}$ Persamaan (1)

Catatan: Tidak hanya molekul di dalam silinder yang bertabrakan dengan permukaan piston dan dengan demikian mengerahkan kekuatan luar. Udara di sekitar luar silinder juga mengandung partikel. Partikel-partikel ini karena itu juga memberikan gaya berlawanan pada piston, yang diarahkan ke dalam. Hanya perbedaan antara kedua gaya yang sesuai dengan gaya yang diperlukan untuk menahan piston pada posisinya. Demi kesederhanaan, ruang hampa di luar silinder diasumsikan sebagai berikut, sehingga gaya Fdalam persamaan (1) dapat dikaitkan secara eksklusif dengan partikel gas di dalam silinder.

Variabel yang mempengaruhi tekanan gas

Tekanan gas dalam silinder akan semakin tinggi semakin banyak partikel bertabrakan dengan piston dalam waktu tertentu. Ini tergantung pada jumlah partikel dalam silinder. Ini karena semakin banyak partikel totalnya, semakin banyak dapat bertabrakan dengan permukaan piston dan akan mengerahkan (dampak) gaya. Ini sudah ditunjukkan oleh pengalaman sehari-hari ketika menggembungkan ban sepeda: semakin banyak udara dipompa ke dalam ban (yaitu semakin banyak partikel di dalamnya), semakin besar tekanan!

Di sisi lain, tekanan gas tergantung pada kecepatan di mana partikel-partikel mengenai permukaan piston. Semakin besar kecepatan, semakin kuat tabrakan dan semakin besar kekuatan tumbukan atau tekanan yang terkait. Ini, juga, ditunjukkan oleh pengalaman sehari-hari: Jika botol diisi dengan udara ditempatkan di bawah sinar matahari, tekanan dalam botol akan meningkat ketika suhu naik, karena kecepatan molekul meningkat dengan suhu yang lebih tinggi.

Perhitungan tekanan gas

Untuk menentukan tekanan gas dalam silinder, jumlah partikel yang bertabrakan dengan piston dalam waktu tertentu Δt.

Secara umum, kecepatan suatu partikel terdiri dari tiga komponen (komponen x-, y- dan z), di mana hanya komponen kecepatan yang dengannya partikel mengenai permukaan piston relevan untuk pembentukan tekanan, yaitu kecepatan dalam arah-x.

Kecepatan partikel-partikel gas yang terdistribusi secara acak

Pertama, diasumsikan bahwa komponen-x dari kecepatan identik untuk semua partikel (|vx|). Karena tidak ada arah yang disukai oleh partikel, setengah dari semua partikel akan bergerak dengan kecepatan ini |vx| dalam arah x positif dan setengah lainnya di arah x negatif.

Namun, tidak semua partikel yang bergerak ke arah positif benar-benar dapat mencapai permukaan piston dalam waktu yang ditentukan Δt. Dengan diasumsikan kecepatan konstan |vx| partikel hanya bisa menempuh jarak maksimum Δsdalam waktu Δt:

$\Delta s=|V_{x}|\cdot \Delta t$ Persamaan (2)

Ini berarti, sebaliknya, hanya partikel yang kurang dari Δs jauh dari piston dapat mengenai permukaan (lihat volume kuning Vc pada gambar di atas). Semua partikel lain tidak akan punya waktu untuk mencapai piston dalam waktu Δt.

Karena partikel terdistribusi secara merata di dalam silinder, maka kepadatan partikel di dalam silinder N/V (rasio jumlah total partikel N dan volume silinder total V) dapat digunakan untuk menentukan jumlah partikel Nc terkandung dalam tekanan yang relevan volume tabrakan Vc sebagai berikut:

$N_{c}=\frac{N}{V}\cdot V_{c}$ persamaan (3)

Sekarang harus dipertimbangkan bahwa hanya setengah dari partikel dalam volume tumbukan yang benar-benar bergerak menuju piston dalam arah x positif. Untuk jumlah partikel Nx dalam volume tumbukan yang benar-benar terbang ke arah piston, hal berikut ini berlaku:

$N_{x}=\frac{1}{2}\cdot N_{c}=\frac{1}{2}\cdot\frac{N}{V}\cdot V_{c}$ Persamaan (4)

Volume tumbukan Vcrelevan untuk pembentukan hasil tekanan dari produk area piston Adan jarak Δs. Dengan demikian, tekanan sejumlah partikel N yang relevanx dalam suara tabrakan dapat dihitung sebagai berikut:

Persamaan (5)

Persamaan ( 6) menunjukkan bahwa gaya pada piston tidak tergantung pada periode waktu yang dianggap Δt! Jika ini masalahnya, tekanannya harus berubah seiring waktu. Namun, pengalaman sehari-hari menunjukkan bahwa tekanan dalam gas tetap konstan selama tidak ada perubahan seperti peningkatan suhu atau pengurangan volume!

Impuls |δp| identik untuk setiap partikel, karena diasumsikan bahwa semua partikel bergerak dengan kecepatan yang sama |vx| dan bahwa tumbukan dengan piston sepenuhnya elastis tanpa kehilangan energi (kinetik). Sebuah partikel yang bergerak menuju piston dengan kecepatan |vx| akan bergerak setelah tumbukan ke arah yang berlawanan dengan kecepatan yang sama |vx|. Karena momentum partikel sebelum tumbukan adalah +m|vx| dan setelah tabrakan -m|vx|, momentum telah berubah dua kali lipat nilainya:

$|\Delta p|=2\cdot m\cdot |v_{x}|$ persamaan (7)

(Analogi: Jika suhu berubah dari -20 ° C menjadi +20 ° C, maka totalnya telah berubah sebesar 40 ° C, yaitu dengan dua kali nilainya).

Jika persamaan (7) sekarang digunakan dalam persamaan (6), maka total gaya Ftot bahwa gas yang diberikan pada piston dapat dihitung dengan rumus berikut:

Catatan: Karena kecepatan vxdikuadratkan dalam persamaan ( 8), tidak perlu lagi menghitung nilai absolut, karena kuadrat dari angka negatif selalu positif.

Karena kekuatan |Ftot|diberikan pada permukaan piston A, tekanan gas berikut haldiperoleh dengan persamaan (1):

Persamaan (9)

Sekarang harus dipertimbangkan bahwa bahkan dalam gas ideal tidak semua molekul memiliki kecepatan yang sama dalam arah x, tetapi didistribusikan secara statistik (secara acak). Karena itu, sesuai dengan persamaan (9), rata-rata aritmatika dari kuadrat kecepatan $\overline{v_{x}^{2}}$ harus dihitung:

$p=\frac{N}{V}\cdot m\cdot \overline{v_{x}^{2}}$ Persamaan (10)

Bukan kecepatan rata-rata (kecepatan rata-rata aritmatika) dari partikel yang dapat dikuadratkan tetapi kuadrat dari kecepatan individu harus dirata-ratakan. Karena itu orang berbicara juga tentang kecepatan kuadrat rata-rata.

Sebagai contoh, tabel di bawah ini menunjukkan untuk 5 partikel hasilnya, jika sekali kecepatan rata-rata (kecepatan rata-rata aritmatika) kuadrat dan setelah kuadrat kecepatan rata-rata (kecepatan kuadrat rata-rata). Jadi kecepatan rata-rata dalam kasus ini adalah 3m/s dan kuadratnya adalah 9m²/s². Jika, di sisi lain, rata-rata kuadrat kecepatan dihitung, nilai 11,8m²/s² diperoleh.

Particle	Speed v in ms	Square of the speeds v2 in m2s2
A	1	1
B	3	9
C	3	9
D	2	4
E	6	36
arithmetic mean	v¯¯¯=3ms	v2¯¯¯¯¯=11,8m2s2

Perhatikan notasi yang berbeda antara kuadrat dari kecepatan rata-rata $\overline{v}^{2}$ dan rata-rata kuadrat kecepatan $\overline{v^{2}}$ .

Hubungan antara gerak dalam arah x dan total gerakan
Pendekatan kinematik

Kecepatan $|\vec{v}|=v$ molekul pada dasarnya dapat ditentukan sebagai berikut dari komponen kecepatannya dalam arah x, y dan z:

$v=\sqrt{v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}$ Persamaan (11)

Untuk kuadrat kecepatan v² oleh karena itu berlaku:

$v^{2}=v_{x}^{2}+v_{y}^{2}+v_{z}^{2}$ Persamaan (12)

Rata-rata kecepatan kuadrat kemudian dapat ditentukan dari nilai rata-rata komponen kecepatan kuadrat individu sebagai berikut:

$\overline{v^{2}}=\overline{v_{x}^{2}}+\overline{v_{y}^{2}}+\overline{v_{z}^{2}}$ Persamaan (13)

Komponen kecepatan molekul terdistribusi secara statistik dan tidak ada arah yang disukai. Nilai rata-rata kuadrat kecepatan akan sama untuk semua komponen kecepatan:

$\overline{v_{x}^{2}}=\overline{v_{y}^{2}}=\overline{v_{z}^{2}}$ Persamaan (14)

Dengan demikian hubungan berikut antara rata-rata kecepatan kuadrat dari partikel $\overline{v_{}^{2}}$ dan nilai rata-rata komponen kecepatan kuadrat dalam arah $\overline{v_{x}^{2}}$ diperoleh:

$\overline{v_{}^{2}}=\overline{v_{x}^{2}}+\overline{v_{x}^{2}}+\overline{v_{x}^{2}}=3\cdot \overline{v_{x}^{2}}$ Persamaan (15)

Rata-rata kecepatan kuadrat dalam arah-x dengan demikian sesuai dengan sepertiga dari kecepatan kuadrat partikel individu:

$\overline{v_{x}^{2}}=\frac{\overline{v_{}^{2}}}{3}$ Persamaan (16)

Jika persamaan (16) diterapkan dalam persamaan (10), maka hubungan berikut antara tekanan gas pdan rata-rata kuadrat kecepatan $\overline{v_{}^{2}}$ partikel individu menjadi jelas:

$p=\frac{1}{3}\cdot \frac{N}{V}\cdot m\cdot \overline{v^{2}}$ Persamaan (17)

Perhatikan bahwa kecepatan v tidak lagi terbatas pada arah-x tetapi mewakili kecepatan total partikel (tepatnya: dengan rata-rata kuadrat kecepatan semua molekul)!

Pendekatan energetik
Hubungan yang sama seperti yang dinyatakan dalam persamaan (17) juga dapat diperoleh dengan pertimbangan energetik. Titik awal adalah persamaan lagi (10). Jika persamaan (10) diperluas dengan faktor 2, maka istilah $\frac{1}{2} m\overline{v_{x}^{2}}$ dapat diartikan sebagai energi kinetik rata-rata $\overline{W_{kin,x}^{}}$ dari partikel yang terkait dengan arah-x:

Persamaan (18)

$p=2\cdot \frac{N}{V}\cdot \overline{W_{kin,x}^{}}$ Persamaan (19)

Karena kecepatan didistribusikan secara acak dan tidak ada arah yang disukai, distribusi kecepatan yang sama diperoleh untuk arah apa pun. Ini pada gilirannya berarti bahwa energi kinetik rata-rata dari partikel di setiap arah adalah identik (yaitu energi kinetik rata-rata yang akan dihasilkan jika gerakan partikel hanya diamati sepanjang satu arah spasial):

$\overline{W_{kin,x}^{}}=\overline{W_{kin,y}^{}}=\overline{W_{kin,z}^{}}$ Persamaan (20)

Namun, partikel tidak hanya bergerak dalam satu arah tetapi dalam ruang tiga dimensi. Total energi kinetik rata - rata $\overline{W_{kin}^{}}$ , yang dimiliki molekul selama gerakan tiga dimensi mereka, adalah jumlah dari energi kinetik sepanjang tiga arah spasial. Karena energi kinetik rata-rata sepanjang arah spasial yang berbeda adalah identik, energi total sesuai dengan tiga kali energi kinetik dalam satu arah spasial (misalnya dalam arah x):

$\overline{W_{kin}^{}}=\overline{W_{kin,x}^{}}+\overline{W_{kin,y}^{}}+\overline{W_{kin,z}^{}}=3\cdot\overline{W_{kin,x}}$ Persamaan (21)
$\cdot\overline{W_{kin,x}}=\frac{1}{3}\cdot\overline{W_{kin}}$ Persamaan (22)

Dengan demikian tekanan dihubungkan sebagai berikut dengan energi kinetik rata-rata suatu partikel (masukkan persamaan (22) di (19)):

$P=2\cdot \frac{N}{V}\cdot \frac{1}{3}\overline{W_{kin}}$ Persamaan (23)

$P=2\cdot \frac{N}{V}\cdot \overline{W_{kin}}$ Persamaan (24)

Tekanan gas bergantung pada jumlah partikel dan volume hanya pada energi kinetik rata-rata suatu partikel!

Perhatikan bahwa energi kinetik rata-rata suatu partikel hanya merujuk pada gerak translasi. Partikel-partikel gas umumnya juga memiliki gerakan rotasi dan karena itu energi rotasi, tetapi ini tidak berpengaruh pada tekanan!

Karena energi kinetik rata-rata partikel dihubungkan oleh massanya ke rata-rata kuadrat kecepatan ( $\overline{W_{kin}}=\frac{1}{2}m\cdot \overline{v^{2}}$ ), dimana kecepatan v tidak lagi hanya mengacu pada arah spasial tetapi pada kecepatan total, maka hubungan yang sama seperti pada persamaan (17) menjadi jelas:

Persamaan (25)

Persamaan (26)

Interpretasi mikroskopis suhu

Dalam artikel " Hukum gas ideal " persamaan berikut diturunkan secara eksperimental:

$p\cdot V=N\cdot K_{b}\cdot T$ Persamaan (27)

Dalam persamaan ini, kB menunjukkan konstanta Boltzmann dan T suhu termodinamika gas. Jika sekarang Anda bawa volume gas Vdalam persamaan (24) di sisi kiri…

$p\cdot V=\frac{2}{3}\cdot N\cdot \overline{W_{kin}}$ Persamaan (28)

… Dan kemudian menyamakan persamaan (27) dan (28), maka hubungan antara energi kinetik rata-rata partikel dan suhu gas menjadi jelas:

Persamaan (29)

Persamaan (30)

Energi kinetik rata-rata partikel hanya bergantung pada suhu!

Juga pada titik ini, energi kinetik sekali lagi hanya merujuk pada gerak translasi dan bukan pada gerak rotasi. Energi rotasi (energi kinetik sudut) tidak mempengaruhi suhu sama sekali!

Energi internal gas ideal

Karena menurut persamaan (30) setiap partikel membawa (rata-rata) energi kinetik $3/2_{}k_{b}T$ , energi total semua partikel dan dengan demikian energi gas dapat diperoleh dengan mengalikan energi kinetik rata-rata suatu partikel dengan jumlah total partikel N. Energi total di dalam gas ini juga disebut energi internal U:

Persamaan (31)

Jika ungkapan NkBT digantikan oleh pV menurut persamaan (27), maka tekanannya juga dapat ditentukan dari kepadatan energi ubdari gas (untuk menghindari kebingungan dengan energi internal spesifik ub sebagai kuantitas terkait massa, "v" ditambahkan ke kepadatan energi volumetrik dalam indeks):