Cara Menghitung Torsi
Ketika mempelajari bagaimana objek berputar, dengan cepat menjadi perlu untuk mengetahui bagaimana gaya yang diberikan menghasilkan perubahan dalam gerakan rotasi. Kecenderungan gaya untuk menyebabkan atau mengubah gerakan rotasi disebut torsi , dan itu salah satu konsep paling penting untuk dipahami dalam menyelesaikan situasi gerak rotasi.
Arti Torsi
Torsi (juga disebut momen - sebagian besar oleh insinyur) dihitung dengan mengalikan gaya dan jarak. Unit SI torsi yang newton-meter, atau N*m (meskipun unit-unit ini adalah sama seperti Joule, torsi bukanlah pekerjaan atau energi, sehingga hanya harus newton-meter).
Dalam perhitungan, torsi diwakili oleh huruf Yunani Tau: τ.
Torsi adalah besaran vektor, artinya memiliki arah dan besaran. Ini sejujurnya adalah salah satu bagian tersulit dalam bekerja dengan torsi karena torsi dihitung menggunakan produk vektor, yang berarti Anda harus menerapkan aturan tangan kanan. Dalam hal ini, ambil tangan kanan dan keriting jari-jari tangan Anda ke arah rotasi yang disebabkan oleh gaya. Jempol tangan kanan Anda sekarang menunjuk ke arah vektor torsi. (Ini kadang-kadang bisa terasa sedikit konyol, ketika Anda mengangkat tangan dan pantomiming untuk mengetahui hasil dari persamaan matematika, tetapi ini adalah cara terbaik untuk memvisualisasikan arah vektor.)
Rumus vektor yang menghasilkan vektor torsi τ adalah:
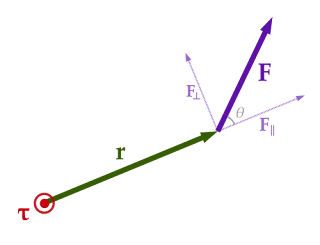
Vektor r adalah vektor posisi sehubungan dengan asal pada sumbu rotasi (Sumbu ini adalah τ pada grafik). Ini adalah vektor dengan besarnya jarak dari mana gaya diterapkan ke sumbu rotasi. Ini menunjuk dari sumbu rotasi menuju titik di mana gaya diterapkan.
- τ = r × F
Besarnya vektor dihitung berdasarkan θ, yang merupakan perbedaan sudut antara r dan F, menggunakan rumus:
- τ = rF sin ( θ )
Kasus Khusus Torsi
Beberapa poin kunci tentang persamaan di atas, dengan beberapa nilai tolok ukur θ :
- θ = 0° (atau 0 radian) - Vektor gaya menunjuk ke arah yang sama dengan r. Seperti yang Anda tebak, ini adalah situasi di mana gaya tidak akan menyebabkan rotasi di sekitar sumbu ... dan matematika membuktikannya. Karena sin (0) = 0, situasi ini menghasilkan τ = 0.
- θ = 180° (atau π radian) - Ini adalah situasi di mana vektor gaya menunjuk langsung ke r . Sekali lagi, mendorong ke arah sumbu rotasi tidak akan menyebabkan rotasi apa pun, dan sekali lagi, matematika mendukung intuisi ini. Karena sin (180°) = 0, nilai torsi sekali lagi τ = 0.
- θ = 90 ° (atau π / 2 radian) - Di sini, vektor gaya tegak lurus terhadap vektor posisi. Ini sepertinya cara paling efektif yang bisa Anda dorong pada objek untuk mendapatkan peningkatan rotasi, tetapi apakah matematika mendukung ini? Nah, sin (90°) = 1, yang merupakan nilai maksimum yang dapat dicapai fungsi sinus, menghasilkan hasil τ = r F. Dengan kata lain, gaya yang diterapkan pada sudut lain mana pun akan memberikan torsi lebih sedikit daripada saat diterapkan pada 90 derajat.
Argumen yang sama seperti di atas berlaku untuk kasus-kasus θ = -90° (atau - π / 2 radian), tetapi dengan nilai dosa (-90 °) = -1 yang menghasilkan torsi maksimum di arah yang berlawanan.
Contoh Torsi
Mari kita perhatikan contoh di mana Anda menerapkan gaya vertikal ke bawah, seperti ketika mencoba melonggarkan mur roda pada ban kempes dengan menginjak kunci pas roda. Dalam situasi ini, situasi ideal adalah memiliki kunci pas horisontal sempurna, sehingga Anda dapat menginjaknya dan mendapatkan torsi maksimum. Sayangnya, itu tidak berhasil. Sebaliknya, kunci pas pas ke mur roda sehingga pada 15% condong ke horizontal. Kunci pas panjang 0,60 m sampai akhir, di mana Anda menerapkan berat penuh 900 N.
Berapa besarnya torsi?
Bagaimana dengan arah ?: Menerapkan aturan "lefty-loosey, righty-tighty", Anda akan ingin mur roda diputar ke kiri - berlawanan arah jarum jam - untuk melonggarkannya. Dengan menggunakan tangan kanan Anda dan melengkungkan jari-jari Anda ke arah berlawanan arah jarum jam, ibu jari mencuat. Jadi arah torsi jauh dari ban ... yang juga arah yang Anda inginkan mur roda akhirnya pergi.
Untuk mulai menghitung nilai torsi, Anda harus menyadari bahwa ada titik yang sedikit menyesatkan dalam pengaturan di atas. (Ini adalah masalah umum dalam situasi ini.) Perhatikan bahwa 15% yang disebutkan di atas adalah kemiringan dari horizontal, tapi itu bukan sudut θ. Sudut antara r dan F harus dihitung. Ada kemiringan 15° dari horizontal ditambah jarak 90° dari horizontal ke vektor gaya ke bawah, menghasilkan total 105° sebagai nilai θ.
Itu satu-satunya variabel yang memerlukan pengaturan, jadi dengan itu di tempat kami hanya menetapkan nilai variabel lainnya:
- θ = 105°
- r = 0,60 m
- F = 900 N
- τ = rF sin ( θ ) =
- (0,60 m) (900 N) sin (105 °) = 540 × 0,097 Nm = 520 Nm
Perhatikan bahwa jawaban di atas hanya mencakup mempertahankan dua angka penting , sehingga dibulatkan.
Akselerasi Torsi dan Sudut
Persamaan di atas sangat membantu ketika ada kekuatan tunggal yang diketahui bekerja pada suatu objek, tetapi ada banyak situasi di mana rotasi dapat disebabkan oleh gaya yang tidak mudah diukur (atau mungkin banyak gaya seperti itu). Di sini, torsi sering tidak dihitung secara langsung, tetapi sebaliknya dapat dihitung dengan mengacu pada percepatan sudut total , α, yang dialami objek. Hubungan ini diberikan oleh persamaan berikut:
- Σ τ - Jumlah total semua torsi yang bekerja pada objek
- I - momen inersia , yang merepresentasikan resistensi objek terhadap perubahan kecepatan sudut
- α - percepatan sudut